上篇文章讲述了贝叶斯定理的历史及作用,那到底什么是贝叶斯定理呢?就长下面这样。
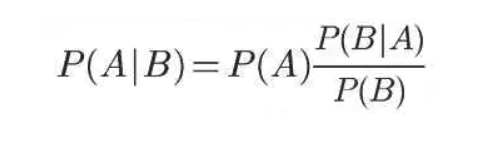
看到这,你肯定希望我说人话吧。举个例子:我的朋友小鹿说,他的女神每次看到他的时候都冲他笑,他想知道女神是不是喜欢他呢?下面我们一起用贝叶斯帮小鹿预测下女神喜欢他的概率有多大,这样小鹿就可以根据概率的大小来决定是否要表白女神。
首先,我分析了给定的已知信息和未知信息:①要求解的问题:女神喜欢你,记为A事件;②已知条件:女神经常冲你笑,记为B事件。所以说P(A|B)是女神经常冲你笑这个事件(B)发生后,女神喜欢你(A)的概率。
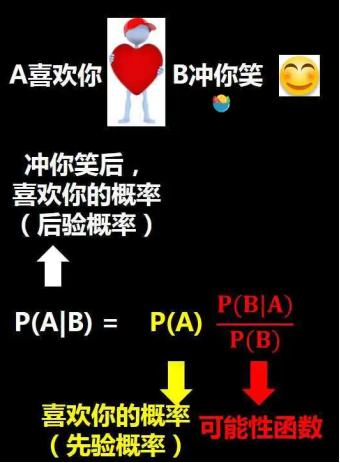
从公式来看,我们需要知道这么3个事情:
(1)先验概率
我们把P(A)称为‘先验概率',即在不知道B事件的前提下,我们对A事件概率的一个主观判断。这个例子里就是在不知道女神经常对你笑的前提下,来主观判断出女神喜欢一个人的概率,这里我们假设是50%,也就是可能喜欢你,可能不喜欢你的概率都是一半。
(2)可能性函数
P(B|A)/P(B)称为‘可能性函数',这是一个调整因子,即新信息B带来的调整,作用是使得先验概率更接近真实概率。可能性函数你可以理解为新信息过来后,对先验概率的一个调整。比如我们刚开始看到“人工智能”这个信息,你有自己的理解(先验概率/主观判断),但是当你学习了一些数据分析,或者看了些这方面的书后(新的信息),然后你根据掌握的最新信息优化了自己之前的理解(可能性函数/调整因子),最后重新理解了“人工智能”这个信息(后验概率)。
如果‘可能性函数'>1,意味着‘先验概率'被增强,事件A的发生的可能性变大;如果‘可能性函数'=1,意味着B事件无助于判断事件A的可能性;如果‘可能性函数’<1,意味着‘先验概率’被削弱,事件A的可能性变小。
还是刚才的例子,根据女神经常冲你笑这个新的信息,我调查走访了女神的闺蜜,最后发现女神平日比较高冷,很少对人笑。所以我估计出‘可能性函数'P(B|A)/P(B)=1.5(具体如何估计,省去1万字)
(3)后验概率
P(A|B)称为‘后验概率',即在B事件发生之后,我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后,对女神喜欢你的概率重新预测。带入贝叶斯公式计算出:
P(A|B)=P(A)* P(B|A)/P(B)=50% *1.5=75%
因此,女神经常冲你笑,喜欢上你的概率是75%。这说明,女神经常冲你笑这个新信息的推断能力很强,将50%的‘先验概率'一下子提高到了75%的‘后验概率'。

在得到预测概率后,小鹿自信满满的发了下面的表白微博。稍后,果然收到了女神的回复。预测成功。
现在我们再看一遍贝叶斯公式,你现在就能明白这个公式背后的最关键思想了:我们先根据以往的经验预估一个‘先验概率'P(A),然后加入新的信息(实验结果B),这样有了新的信息后,我们对事件A的预测就更加准确了。
其实阿尔法狗也是这么战胜人类的,简单来说,阿尔法狗会在下每一步棋的时候,都可以计算自己赢棋的最大概率,就是说在每走一步之后,他都可以完全客观冷静的更新自己的信念值,完全不受其他环境影响。
以上是对贝叶斯定理的简单介绍,若对此感兴趣,可以查阅相关文章来详细了解。
参考资料:

