大家都知道,计算机智能识别0和1的二进制数,对于复杂的逻辑判断也只通过它来实现,这就是经典的布尔逻辑。
布尔数值就是0和1,是和非,也是计算机逻辑的基础
。
其基本运算就是
“
与、或、非
”
,体现在编程中就是“If ...
then...”,我们大部分的自动化程序就是用布尔逻辑设计的。
布尔逻辑赋予计算机自动判断和决策的能力,但是却并不完美,甚至限制了计算机的能力,因为人类判断和决策往往没那么简单。比如布尔逻辑能够很好地处理那种逻辑非常清晰的场景,比如用电脑可以轻松编写“如果下雨就提醒我出门带伞”这样的程序,因为下不下雨是一个清晰的是“非”逻辑,人在实际决定带不带伞出门时常是考虑雨的大小,雨会下多久。那多大的雨算大雨需要带伞,多小的雨算小雨不用带伞呢?对于人类的决策来说往往没有一个清晰的雨量的门槛。模糊逻辑就是用来解决这样的分类和决策难题的。
在模糊逻辑的眼中,大雨,小雨,和中雨之间是没有严格的界限的,也就是说某一种雨量的大小并不完全归属于某一个类,而是以隶属度来衡量的。比如对于10mm降雨,隶属于小雨的隶属度为0.5,中雨的隶属度为0.4,大雨的隶属度为0.1;对于100mm降雨,小雨的隶属度为0,中雨的隶属度为0.3,大雨的隶属度为0.7。
将逻辑的输入数值(降雨量)转化成各个集合(小雨,中雨,大雨)的隶属度的过程就叫做Fuzzification。 也是模糊逻辑的第一步。
那应该如何确定输入数值与隶属度的关系呢?这就要用到隶属度函数了。通常可以用下图这种方式表示。
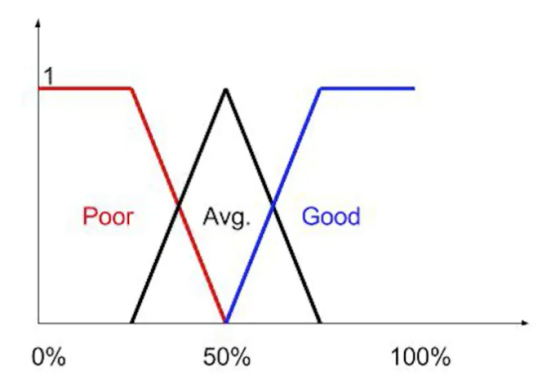
上图是考试分数和学生成绩的隶属度关系。比如考0分,Poor的隶属度为1,Avg. 和Good为0。 考试为32.5分(红黑交叉点),Poor的隶属度为0.5,Avg.为0.5, Good为0。 在任意一点都能找到其所对应的集合的隶属度。
模糊逻辑的运算实际上就是模糊逻辑中分解出的各个隶属度的运算。我们将逻辑的两个输入定义为A,B,输出为C(A与B -> C),举个例子,A = Poor: 0.5(Poor的隶属为0.5 )B = Good:0.2,那么C= A与B是多少呢?其实有好多计算C的方法,这里介绍一个最简单的“最小隶属法(MIN implication)”,于是 C=A与B中最小那个(0.2)。于是C= Good: 0.2.那D = A或B怎么计算呢?还是介绍一个最简单的“最大隶属法(MAX implication)”,即 C=A或B中最大的那个(0.5)。于是D= Poor: 0.5。“非”的运算就更简单了,直接如下图所示取相反的折线就完了。
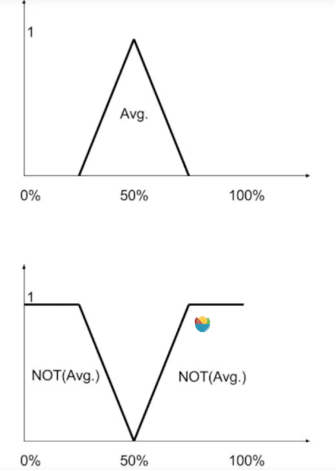
将输入模糊化了之后,则需要通过规则,和模糊逻辑的运算来重新组合,并得到相应的输出值,这些输出我们在模糊逻辑中定义为Fire Strength(FS)(此处不再详述规则,感兴趣的同学可自行了解)。
模糊逻辑通过模糊化将输入的数值转化成各个集合的隶属度之后,再通过规则和运算可以得到若干个FS。这些FS并不能为我们解决实际问题。我们想知道给出任意输入值能输出一个确定的数值,这时我们就要用去模糊化来得到这个输出值了。
同样地,去模糊化有很多方法,这里我同样只介绍一个简单和应用广泛的方法:加权平均判决法,公式如下图(仅做了解,不细述)
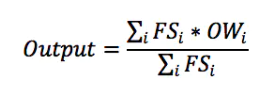
就此大概介绍了模糊逻辑的基本内容,整体框架理解起来感觉还是不难的。模糊逻辑已经广泛应用在电冰箱,电饭锅等自动控制,同时还广泛运用在了游戏的开发中。
参考资料:

