傅里叶变换是一种线性积分变换，用于信号在时域和频域之间的变换，在物理学和工程学应用颇多。实际上傅里叶变换就像化学分析，确定物质的基本成分。举例来说，傅里叶能将一段美妙的音乐，还原成乐谱。

傅里叶生平

 

 

约瑟夫·傅里叶于1768年3月21日在法国约讷省欧塞尔出生。幼年时父母双亡，所以很小便被送入天主教本笃会接受教育，之后考入巴黎高等师范学校，毕业后在军队中教授数学。1795年他到巴黎高等师范学校教书，之后又任聘为巴黎综合理工学院教授。

1798年他跟随拿破仑东征，被任命为下埃及的总督。由于英国舰队对法国人进行了封锁，所以他受命在当地生产军火为远征部队提供军火。这个时期，他向开罗埃及学院递交了几篇有关数学的论文。1801年，拿破仑远征军队失败后，他便被任命为伊泽尔省长官。1809年被封为男爵。1816年他回到巴黎，六年后他当选了科学院的秘书，并发表了《热的分析理论》一文，此文是建立在牛顿的热传导理论的速率和温度差成正比的基础上。

1830年5月16日他病逝于巴黎，1831年他的遗稿被整理出版成书。

数学上的重大突破

 

傅里叶在研究热传递的过程中，在其论文中声明，一个变量的任意函数，不论是否连续或不连续，都可展开为正弦函数的级数，而这正弦函数的参数为变量的倍数。虽然这个声明在现在看来并不完全正确，但是正是有了这个思路，数学才能得以突破。因此，傅里叶变换的命名，也是为了纪念这位伟大的数学家。

什么叫频域

 

要学习傅里叶变换，首先需要认识频域。我们日常生活中看到的大部分信息，都是以时间贯穿的，例如股票的走势，汽车的轨迹。这种以时间作为参照来观察动态世界的方法，我们称其为时域分析。在时域分析中，我们看到的一切都是在变化的。但是万变不离其宗，所有变化的事物，都有其不变的内核。优美的旋律归根结底也就是音符的排列组合，普通话归根结底还是汉语拼音字母组成。频域，也就相当于音乐中的音符，普通话中的字母，都是最基本的组成成分。任由你长篇大论，在频域眼中，不过是声母、韵母、整体连读音节。

 

傅里叶变换

都说傅里叶变换能对时域频域进行转换，而傅里叶变换是基于傅里叶级数的，所以先来了解一下什么是傅里叶级数。傅里叶级数表明，复杂的周期函数可以用一系列简单的正弦、余弦波之和表示。

 

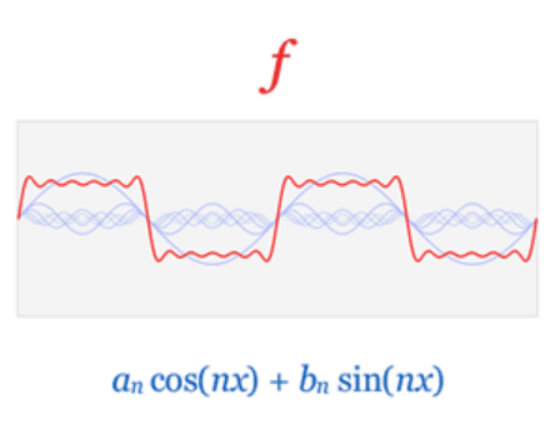
【时域方向的信号】

 

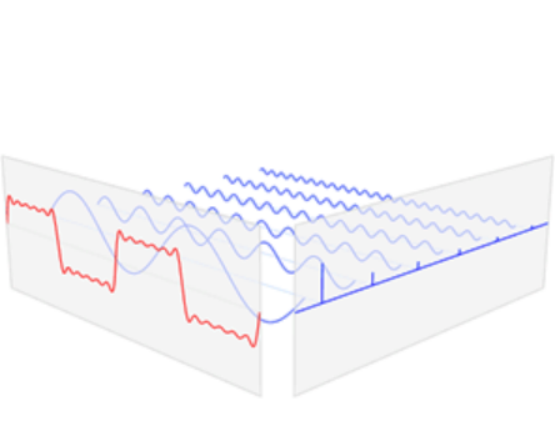
【傅里叶级数分解时域方向的信号】

 

【频域方向的信号】

经过傅里叶级数，时间方向我们看到的信号，究其本质，是由无穷个不同频率的信号所组成的。

傅里叶变换

傅里叶变换实质是对傅里叶级数的扩展，傅里叶级数处理的对象是复杂周期函数，傅里叶变换的对象则是周期趋近于无限的函数。

比如傅里叶级数，在时域是一个周期且连续的函数，而在频域是一个非周期离散的函数。

而在我们接下去要讲的傅里叶变换，则是将一个时域非周期的连续信号，转换为一个在频域非周期的连续信号。

 

 

    至此，傅里叶变换简单介绍完毕 。 虽然过程曲折还有些许难懂，但最重要 的是， 我们 需 要明白傅里叶变换是用来干什么的，而且要有一种透过事物看本质的思想。也就是说，学过了傅里叶变换以后，在喝可乐的时候，知道傅里叶变换能让你懂得可乐的配方。在听音乐的时候，傅里叶变换能给你写出音乐的音谱。吃妈妈煮的菜，傅里叶变换能让你知道妈妈用了什么食材，何种调味料。

参考资料：

 

[1]韩昊.傅里叶分析之掐死教程（完整版）更新于2014.06.06[EB/OL].https://zhuanlan.zhihu.com/p/19763358,2014-06-06.